Is this AI developing a sense of time?

In what way can one speak of a computer developing a sense of time? That's an intriguing question proposed by new research from the Ruprecht-Karls-Universität in Heildelberg and cooperating institutions that tries to create in a neural network the "arrow of time."
The arrow of time, coined by astronomer Arthur Eddington, is the notion that time has a direction, a sense that states of affairs transition from one to another along a trajectory, and don't reverse that trajectory. You might think of knocking over a vase from a table. With the vase lying in pieces on the floor, the prior state, where it's intact on the table, is now unreachable, giving people a sense of time's passage.
Can a computer be endowed with that fact about the physical world?
Lead author Nasim Rahaman and colleagues developed a neural network that modifies what's known as reinforcement learning, the pursuit of actions leading to goals. The network computes the likelihood that once a given state of affairs leads to another, the process is not likely to be reversed to the earlier state.
As they write, "We humans seem to have an innate understanding of the asymmetric progression of time, which we use to efficiently and safely perceive and manipulate our environment.
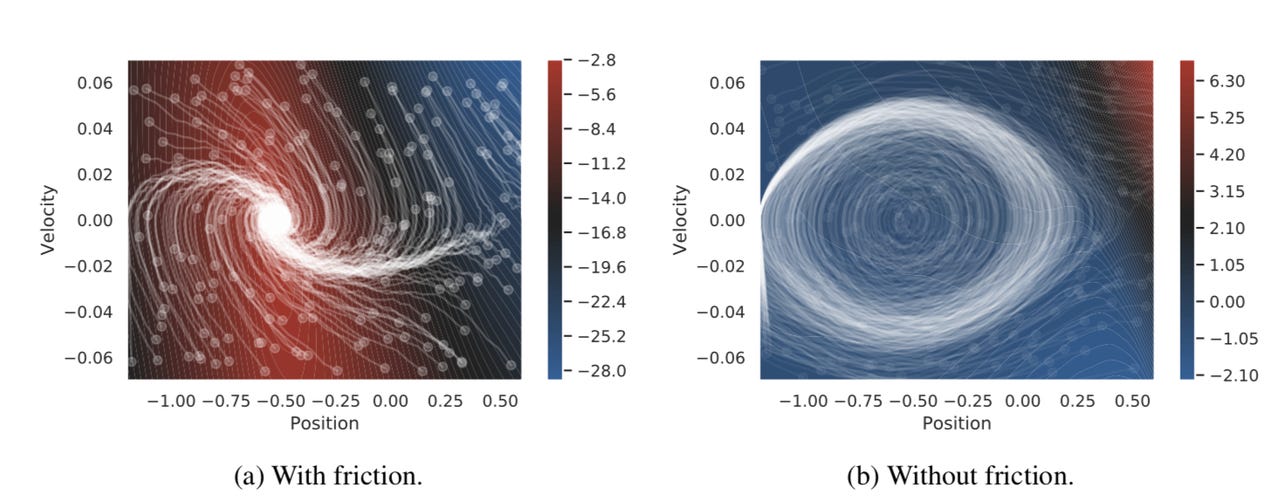
Rahaman et al. compute the "h-potential" in a game where a car is moved over a mountain landscape. The presence of friction in the car's progress adds up to dissipation in the model of the game, represented as the bright red h-potential at a certain point in the car's position and velocity.
"We ask whether and how these properties can be exploited to learn a representation that functionally mimics our understanding of the asymmetric nature of time."
The result of the research is not a sense of time in the way we colloquially think of it. Instead, the computer is able to compute the necessary order of states of affairs. The capability, the authors argue, could improve reinforcement learning for things such as making sure that artificial intelligence doesn't cause unintended effects (imagine A.I. acting in a medical application.)
Also: IBM's AI flies back and forth through time in Flappy Bird
The paper, "Learning the Arrow of Time," is posted on the arXiv pre-print server, and is co-authored by Rahaman, who holds multiple appointments at Ruprecht-Karls-Universität, Montreal's prestigious MILA institute for machine learning, and the Max-Planck Institute for Intelligent Systems; Steffan Wolf and Roman Remme of Ruprecht-Karls; and Anirudh Goyal and Yoshua Bengio of MILA. Bengio, you'll note, is one of three recipients of this year's ACM Turing Award for achievement in computing.
The authors used a form of reinforcement learning called Q-Learning. The important part is that unlike the game of chess or go, where reinforcement learning is helped by knowing the rules of the game, in this work, the rules aren't known. A computer is input with various states of an environment with no knowledge of how one state may lead to another. The computer has to compute which different states can be reached from one another and which cannot, a measure of the irreversibility of taking action.
An example is what's known as the "2D world with vases." The computer can move a virtual agent around a grid of tiles toward a goal located somewhere in the grid. As it moves, it encounters vases on some of the tiles. If it encounters one, the vase disappears from the grid, representing the vase having been broken by, one imagines, the virtual agent tipping the vase off its little table. That change, the vase disappearing and never reappearing, means the prior state, a tile with a vase, is no longer reachable.
Exploring in this way, the computer is transforming the beginning state of the grid, where there's no information about what states entail one another, into a comprehensive map of what states can be reached and what states become unreachable because of a broken vase. In formal terms, the computer is calculating a function called the "h-potential," symbolized by the letter "h" in equations, which increases as the number of states in the game grid with broken vases increases. This h-potential is then used to construct a "reachability" measure, symbolized by the Greek letter "η," ita. Reachability then becomes a matter of computing how actions lead to states with higher h-potential.
- What is AI? Everything you need to know
- What is deep learning? Everything you need to know
- What is machine learning? Everything you need to know
- What is cloud computing? Everything you need to know
All this has a variety of practical applications. For example, it can be a way to build A.I. systems with fewer unintended side-effects, such as in the medical example.
But just what is learned, exactly? In theory, the authors show that this model of states of affairs — computing the increase in h-potential, and the reachability change, and therefore the irreversibility of states of affairs — agrees with fundamental physics. Specially, predictions by their program agree with the "free-energy function" of statistical physics concerning how particles undergo Brownian motion. You can think of physics as the "ground truth," or, as the authors put it, "the true arrow of time."
But there are other things about time that don't factor in here. For example, computing reachability doesn't make clear anything about causality. A computer hasn't calculated anything like a model for how vases are broken. And a sense of causality is arguably part of a human's sense of the arrow of time.
As the authors write in their concluding remarks, "Future work could draw connections to algorithmic independence of cause and mechanism and explore applications in causal inference."